La somme des angles d'un triangle. Le théorème de la somme des angles d'un triangle

Le triangle est un polygone ayant trois côtés (trois angles). Le plus souvent, la partie désignée par des lettres minuscules lettres majuscules correspondantes, qui représentent des sommets opposés. Dans cet article, nous examinons ces types de formes géométriques, théorème, qui définit ce qui est égal à la somme des angles d'un triangle.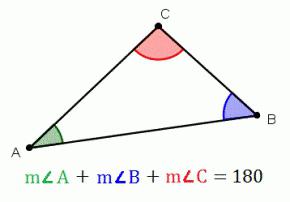

Types plus angles

Les types de polygone avec trois sommets suivants:

• à angle aigu, dans lequel tous les angles sont tranchantes;
• rectangulaire ayant une angle droit, le côté formant elle, fait référence aux jambes, et le côté qui est disposé opposé à l'angle droit est appelé l'hypoténuse;
• obtus lorsque l' un angle est obtus ;
• isocèle dont les deux côtés sont égaux et ils sont appelés latérale, et le troisième – un triangle avec une base;
• ayant équilatéral trois côtés égaux.

propriétés

Affecter les propriétés fondamentales qui sont caractéristiques de chaque type de triangle:

• en face du plus grand côté est toujours plus grand angle, et vice versa;
• sont des angles égaux opposés de la même plus grande partie, et vice versa;
• dans un triangle a deux angles aigus;
• angle extérieur supérieur à un angle quelconque interne de celui-ci non adjacent;
• la somme de toutes les deux angles est toujours inférieur à 180 degrés;
• angle extérieur est égal à la somme des deux autres coins, qui ne sont pas mezhuyut avec lui.

Le théorème de la somme des angles d'un triangle

Le théorème dit que si vous mettez tous les coins de la forme géométrique, qui est situé sur un plan euclidien, leur somme sera de 180 degrés. Essayons de démontrer ce théorème.

Laissez-nous un triangle arbitraire avec des sommets KMN. 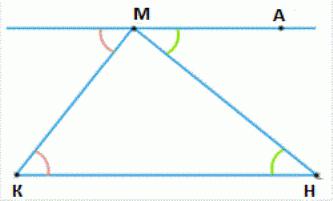Dans la partie supérieure de M tiendra un parallèle direct à la ligne KN (même cette ligne est appelée Euclide). Il convient de noter le point A de sorte que les points k et A sont disposés de différents côtés de la ligne MN. Nous obtenons le même angle d'AMS et MUF, qui, comme l'intérieur, se trouvent en travers pour former intersection MN conjointement avec le CN direct et MA, qui sont parallèles. Il en résulte que la somme des angles du triangle, situés au niveau des sommets de m et n est égale à la taille de l'angle CMA. Les trois angles se composent d'une somme égale à la somme des angles de KMA et MCS. Étant donné que les données sont des angles internes des lignes parallèles face par rapport CL et CM MA en coupant, leur somme est de 180 degrés. Cela prouve le théorème.

résultat

De ce qui précède le théorème ci-dessus implique le corollaire suivant: chaque triangle a deux angles aigus. Pour le prouver, supposons que cette figure géométrique ne comporte qu'un seul angle aigu. Vous pouvez également supposer qu'aucun des coins ne sont pas nettes. Dans ce cas, il doit être d'au moins deux angles, dont la grandeur est égale ou supérieure à 90 degrés. Mais la somme des angles est supérieur à 180 degrés. Mais cela ne peut être, comme d'après les angles de somme de théorème d'un triangle est égal à 180 ° – ni plus, ni moins. C'est ce qui devait être prouvé.

Propriété coins extérieurs

Quelle est la somme des angles d'un triangle, qui sont externes? La réponse à cette question peut être obtenue en appliquant l'une des deux façons. La première est que vous devez trouver la somme des angles, qui sont pris un à chaque sommet, soit trois angles. La seconde implique que vous devez trouver la somme des six angles aux sommets. Pour faire face au début du premier mode de réalisation. Ainsi, le triangle contient six coins extérieurs – dans la partie supérieure de chacun des deux. 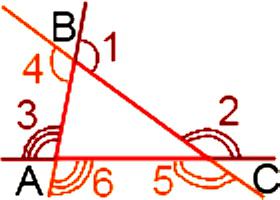Chaque paire a des angles égaux entre eux, car ils sont verticaux:

∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.

De plus, on sait que le coin externe d'un triangle est égale à la somme des deux intérieurs, qui ne sont pas mezhuyutsya avec lui. Par conséquent,

∟1 = ∟A + ∟S, ∟2 = ∟A + ∟V, ∟3 = ∟V + ∟S.

De cela, il semble que la somme des angles extérieurs, qui sont pris un par un près de chaque sommet sera égal à:

∟1 + ∟2 + ∟3 = ∟A + + ∟S ∟A ∟V + + + ∟V ∟S = 2 x (∟A + ∟V ∟S +).

Compte tenu du fait que la somme des angles est égale à 180 degrés, on peut affirmer que ∟A + ∟V ∟S = + 180 °. Cela signifie que ∟1 + + ∟2 ∟3 = 2 x 180 ° = 360 °. Si la deuxième option est utilisée, la somme des six angles sera d'autant plus deux fois. -À-dire la somme des angles d'un triangle à l'extérieur sera:

∟1 + ∟2 + ∟3 + ∟4 + + ∟5 ∟6 = 2 x (∟1 + + ∟2 ∟2) = 720 °.

triangle rectangle

Ce qui correspond à la somme des angles d'un triangle, est l'île? La réponse, encore une fois, résulte du théorème, qui affirme que les angles d'un triangle est jusqu'à 180 degrés. Un son notre affirmation (propriété) comme suit: dans un angle vif triangle ajouter jusqu'à 90 degrés. Nous prouvons sa véracité. 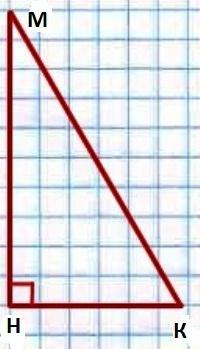Qu'il y ait donné triangle KMN, qui ∟N = 90 °. Il est nécessaire de prouver que ∟K ∟M = + 90 °.

Ainsi, selon le théorème de la somme des angles ∟K + ∟M ∟N + = 180 °. Dans cette condition, il est dit que ∟N = 90 °. Il se trouve ∟K ∟M + + 90 ° = 180 °. C'est ∟K ∟M + = 180 ° – 90 ° = 90 °. Voilà ce que nous devons prouver.

En plus des propriétés ci-dessus d'un triangle rectangle, vous pouvez les ajouter:

• angles, qui se trouvent contre les jambes sont tranchants;
• l'hypoténuse du triangle supérieur à l'une des jambes;
• la somme des jambes plus que l'hypoténuse;
• côté du triangle, qui se trouve opposé à l'angle de 30 degrés, la moitié de l'hypoténuse, qui est égale à sa moitié.

Comme autre propriété de la forme géométrique, on peut distinguer théorème de Pythagore. Selon elle, dans un triangle avec un angle de 90 degrés (rectangulaire), la somme des carrés des jambes est égale au carré de l'hypoténuse.

La somme des angles d'un triangle isocèle

Précédemment, nous avons dit qu'un triangle isocèle est un polygone à trois sommets, contenant deux côtés égaux. Cette propriété est connue figure géométrique: les angles à sa base égale. Prouvons cela.

Prenez le triangle KMN, qui est isocèle, Caroline du Sud – sa base. 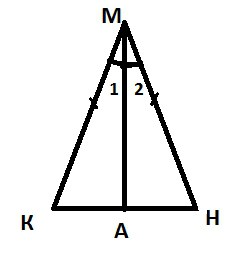Nous sommes tenus de prouver que ∟K = ∟N. Ainsi, supposons que MA – KMN est la bissectrice de notre triangle. triangle ICA avec le premier signe de l'égalité est triangle MNA. A savoir, par hypothèse étant donné que CM = NM, MA est un côté commun, ∟1 = ∟2, parce que MA – ce bissectrice. En utilisant l'égalité des deux triangles, on pourrait dire que ∟K = ∟N. Par conséquent, le théorème est démontré.

Mais nous sommes intéressés à ce que la somme des angles d'un triangle (isocèle). Parce que, à cet égard, il ne dispose pas de fonctionnalités, nous partirons du théorème discuté précédemment. Autrement dit, on peut dire que ∟K + ∟M ∟N + = 180 °, ou 2 x ∟K ∟M + = 180 ° (comme ∟K = ∟N). Ce ne sera pas prouver la propriété, comme le théorème sur la somme des angles d'un triangle a été prouvé plus tôt.

Sauf les propriétés considérées des angles d'un triangle, il y a également des déclarations importantes:

• à une hauteur de triangle equilateral, qui avait été réduit à la base, est simultanément la bissectrice de l'angle médian qui se trouve entre les côtés égaux et l'axe de symétrie de sa base;
• médiane (bissectrice, altitude), qui sont maintenus sur les côtés d'une figure géométrique, sont égaux.

triangle équilatéral

Il est aussi appelé droit, est le triangle, qui sont égaux à toutes les parties. Et donc aussi égaux et angles. Chacun d'eux est de 60 degrés. Prouvons cette propriété.

Supposons que nous avons un triangle KMN. Nous savons que KM = HM = KH. Cela signifie que, selon la propriété des angles situés à la base d'un triangle équilatéral ∟K = ∟M = ∟N. Etant donné que, selon la somme des angles d'un triangle théorème de ∟K + ∟M ∟N + = 180 °, alors x 3 = 180 ° ∟K ou ∟K = 60 °, ∟M = 60 °, ∟N = 60 °. Ainsi, l'affirmation est prouvée. Comme on le voit ci – dessus des éléments de preuve sur la base du théorème ci – dessus, la somme des angles d'un triangle équilatéral, en tant que la somme des angles de tout autre triangle est de 180 degrés. Encore une fois prouver ce théorème n'est pas nécessaire.

Il y a encore quelques propriétés caractéristiques d'un triangle équilatéral:

• hauteur médiane de la bissectrice dans une figure géométrique identique, et leur longueur est calculée comme (a x √3): 2;
• si ce polygone circonscrit le cercle, le rayon sera égal à (a x √3): 3;
• si inscrit dans un cercle triangle équilatéral, son rayon serait (a x √3): 6;
• aire de la figure géométrique est calculée par la formule: (x a2 √3): 4.

triangle obtuse

Par définition, un triangle à angle obtus, l' un de ses coins est compris entre 90 et 180 degrés. Mais compte tenu du fait que les deux autres angles de la forme géométrique forte, on peut conclure qu'ils ne dépassent pas 90 degrés. Par conséquent, le somme des angles d'un triangle théorème fonctionne en calculant la somme des angles d'un triangle obtus. Donc, nous pouvons dire en toute sécurité, sur la base du théorème ci-dessus que la somme des angles obtus d'un triangle est de 180 degrés. Encore une fois, ce théorème n'a pas besoin de re-preuve.