Différentiels – qu'est-ce? Comment trouver la différence de la fonction?

En plus des dérivés leurs fonctions différentiels – il quelques – uns des concepts de base du calcul différentiel, la section principale de l' analyse mathématique. Comme inextricablement liés, les deux d'entre eux plusieurs siècles largement utilisés pour résoudre presque tous les problèmes qui ont surgi au cours de l'activité scientifique et technique.

L'émergence du concept de différentiel

Pour la première fois clairement qu'une telle différence, l'un des fondateurs (avec Isaakom Nyutonom) calcul différentiel célèbre mathématicien allemand Gotfrid Vilgelm Leybnits. Avant que les mathématiciens du 17ème siècle. utilisé très floue et vague idée de quelque infinitésimale « sans partage » de toute fonction connue, ce qui représente une valeur constante très faible mais pas égale à zéro, en dessous duquel les valeurs de la fonction ne peut pas être simplement. Par conséquent, il est seulement une étape pour l'introduction de la notion de tranches infinitésimales d'arguments de la fonction et de leurs tranches respectives des fonctions qui peuvent être exprimées en termes de dérivés de celui-ci. Et cette étape a été presque simultanément les deux grands scientifiques ci-dessus.

Sur la base de la nécessité d'aborder la mécanique pratique urgents problèmes qui se posent à l'industrie la science qui se développe rapidement et la technologie, Newton et Leibniz ont créé les moyens communs de trouver les fonctions du taux de variation (en particulier en ce qui concerne la vitesse mécanique du corps de la trajectoire connue), ce qui a conduit à l'introduction de ces concepts, que la fonction dérivée et l'écart, et ont également trouvé des solutions inverses des algorithmes de problèmes comme connu en soi (variables) les vitesses parcourues pour trouver le chemin qui a conduit au concept de l'intégrale Ala.

Dans les œuvres de Leibniz et l'idée de Newton abord, il est apparu que les écarts – est proportionnelle à l'augmentation des arguments de base incrémente fonctions Δu qui Dh peuvent être appliquées avec succès pour calculer la valeur de celle-ci. En d'autres termes, ils ont découvert qu'une fonction d'augmentation peut être à tout moment (au sein de son domaine de définition) est exprimée par l'intermédiaire de son dérivé à la fois Δu = y « (x) Ah + αΔh où α Ah – reste, ce qui tend vers zéro lorsque Ah → 0, beaucoup plus vite que la réelle Dh.

Selon les fondateurs de l'analyse mathématique, les différences – c'est exactement le premier terme par incréments de toutes les fonctions. Même sans une séquence de concept de limite clairement définis sont compris intuitivement que la valeur différentielle de la dérivée tend à fonctionner lorsque Ah → 0 – Δu / Ah → y « (x).

Contrairement à Newton, qui était avant tout un physicien et un appareil mathématique considéré comme un outil auxiliaire pour l'étude des problèmes physiques, Leibniz accordé plus d'attention à cette boîte à outils, y compris un système de symboles visuels et compréhensibles valeurs mathématiques. Il est celui qui a proposé la notation standard de la fonction des écarts dy = y '(x) dx, dx, et la dérivée de la fonction d'argument que leur relation y' (x) = dy / dx.

La définition moderne

Quelle est la différence en termes de mathématiques modernes? Elle est étroitement liée à la notion d'un incrément variable. Si la variable y prend une première valeur de y y = _1, y = y _2, la différence y ₂ y ₁ ─ est appelée la valeur d'incrément y. 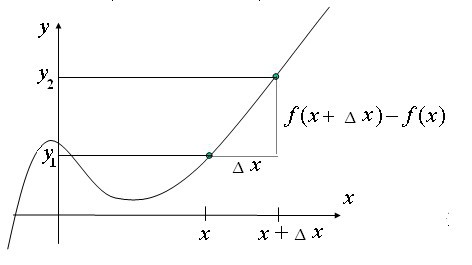L'incrément peut être positif. négative et zéro. Le mot « incrément » est désigné Δ, Δu enregistrement (lecture « delta y ») représente la valeur de l'ordonnée de l'incrément. si Δu = y ₂ ─ y _1.

Si la valeur Δu fonction arbitraire y = f (x) peut être représenté sous la forme Δu = A Ah + α, dans laquelle A représente aucune dépendance sur Ah, t. E. A = const pour le x donné, et le terme α lorsque Ah → 0 tend à il est encore plus rapide que la Ah réelle, alors le premier ( « master ») un terme proportionnel Ah, et différentiel pour y = f (x), désigné dy ou df (x) (lire "y de", "de eff de X"). différentiels Par conséquent – linéaire « principal » par rapport aux composants des incréments fonctions ôh.

explication mécanique

Soit S = f (t) – la distance en se déplaçant en ligne droite point matériel à partir de la position initiale (t – temps de Voyage). Increment As – est le point de passage pendant un intervalle de temps At, et les ds différentielles = f « (t) At – ce chemin, lequel point aurait lieu pendant le même temps At, si elle a conservé le f de la vitesse » (t), atteint à l'instant t . Quand un chemin imaginaire infinitésimale At ds diffère des As réels ayant infinitésimale un ordre plus élevé par rapport à At. Si la vitesse à l'instant t est pas égal à zéro, la valeur approximative ds donne petit point de polarisation.

interprétation géométrique

Soit la ligne L est le graphe de y = f (x). Ensuite Δ x = MQ, Δu = QM « (voir. Figure ci-dessous). Tangent brise MN Δu coupé en deux parties, QN et NM. D'abord et Dh est proportionnelle QN = MQ ∙ tg (angle QMN) = Ah f « (x), t. E QN est différentielle dy.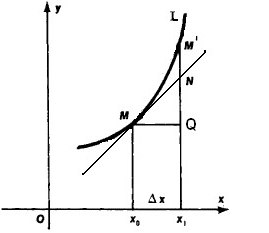

La deuxième partie de la différence Δu NM'daet ─ dy, lorsque → 0 Dh longueur NM « diminue encore plus vite que l'augmentation de l'argument, à savoir qu'il a l'ordre de modicité supérieur à Dh. Dans ce cas, si f « (x) ≠ 0 (tangents non parallèle OX) segments QM'i QN équivalents; en d'autres termes NM 'diminue rapidement (ordre de petitesse de son plus élevé) que l'incrément total de Δu = QM. Ceci est évident sur la figure (segment approchant M'k M NM'sostavlyaet tout petit pourcentage segment » QM).

Ainsi, le différentiel graphiquement fonction quelconque est égale à l'incrément de l'ordonnée de la tangente.

Dérivé et différencié

Un facteur dans le premier terme de la fonction d'augmentation de l'expression est égale à la valeur de sa dérivée f « (x). Ainsi, la relation suivante – dy = f '(x) Ah ou df (x) = f' (x) Ah.

Il est connu que l'augmentation de l'argument indépendant est égal à son différentiel = dx Dh. En conséquence, on peut écrire: f « (x) dx = dy.

Trouver (parfois dit être la « décision ») les écarts est effectuée par les mêmes règles que pour les dérivés. Une liste d'entre eux est donnée ci-dessous.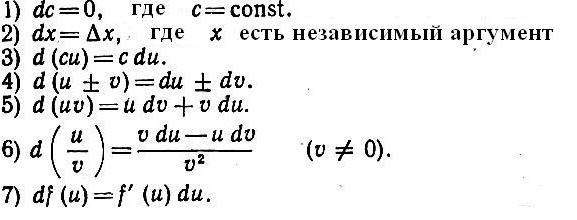

Ce qui est plus universel: l'augmentation de l'argument ou son différentiel

Ici, il est nécessaire d'apporter quelques éclaircissements. La valeur de représentation de f « (x) différentiel Ah possible lorsque l'on considère x comme argument. Mais la fonction peut être un complexe, dans lequel x peut être une fonction de l'argument t. Ensuite, la représentation de l'expression différentielle de f « (x) Ah, en règle générale, il est impossible; sauf dans le cas d'une dépendance linéaire x = at + b.

En ce qui concerne la formule f « (x) dx = dy, puis dans le cas d'argument indépendante x (alors dx = AH) dans le cas de la dépendance paramétrique de x t, il est différentiel.

Par exemple, l'expression 2 x Ah est pour y = x ² son différentiel lorsque x est un argument. Nous maintenant x = t ² et supposons argument t. Alors y = x ² t = ^4.

Ceci est suivi par (t + At) ² = t ² + 2tΔt + ^At2. Par conséquent = 2tΔt + Dh ^At2. Par conséquent: 2xΔh = 2t ² (2tΔt + ^At2).

Cette expression est pas proportionnelle à At, et est donc maintenant 2xΔh non pas différentiel. Il peut être trouvé à partir de l'équation y = x ² t = ^4. Il est égal dy = 4t ³ At.

Si l' on prend l'expression 2xdx, il est le différentiel y = x ² pour tout argument t. En effet, lorsque x = t ² obtenir dx = 2tΔt.

Ainsi 2xdx = 2t ² 2tΔt = 4t ³ At, t. E. Les différences d'expression enregistrées par deux variables différentes coïncident.

Remplacement des écarts par incréments

Si f « (x) ≠ 0, équivalent Δu et dy (lorsque → 0 Dh); si f « (x) = 0 (sens et dy = 0), elles ne sont pas équivalentes.

Par exemple, si y = x ^2, puis Δu = (x + Dh) ² ─ x ² = 2xΔh + ² et dy Dh = 2xΔh. Si x = 3, nous avons Δu = 6Δh + ² et dy Dh = 6Δh qui sont équivalentes à cause ² → 0 Dh, lorsque x = 0 valeur Δu = ² et dy Dh = 0 ne sont pas équivalents.

Ce fait, ainsi que la structure simple de l'écart (m. E. Linéarité par rapport à AH), est souvent utilisé dans le calcul approximatif, en supposant que la dy de Δu pour les petites Ah. Trouver la fonction différentielle est généralement plus facile que de calculer la valeur exacte de l'incrément.

Par exemple, nous avons cube métallique avec bord x = 10.00 cm. En chauffant le bord allongé sur 0,001 cm = Dh. Comment cube augmentation du volume V? Nous avons V = x ^2, de sorte que VQ = 3x ² = 3 Dh ∙ ∙ Février ¹⁰ 0/01 = 3 (cm ^3). L' augmentation différentielle équivalente AV dV, de sorte que AV = 3 cm ^3. calcul complet donnerait ³ = 10,01 ─ AV Mars ¹⁰ = 3,003001. Mais le résultat de tous les chiffres, sauf le premier pas fiable; , Il est donc encore nécessaire d'arrondir à 3 cm ^3.

De toute évidence, cette approche est utile que s'il est possible d'estimer la valeur transmise par erreur.

fonction différentielle: exemples

Essayons de trouver la différence de la fonction y = x ^3, trouver le dérivé. Rendons l'incrément argument Δu et à définir.

Δu = (AH + x) ³ ─ x ³ = 3x ² + Ah (AH 3xΔh ² + ^3).

Ici, le coefficient A = 3x ² ne dépend pas de Dh, de sorte que le premier terme est proportionnelle Dh, l'autre membre 3xΔh ² + ³ Dh → 0 quand Dh diminue plus rapidement que l'augmentation de l'argument. Par conséquent, un élément de 3x ² Ah est la différentielle de y = x ^3:

dy = 3x ² AH = 3x ² dx ou d (x ³⁾ = 3x ² dx.

Dans lequel d (x ³⁾ / dx = 3x ^2.

Dy On trouve maintenant la fonction y = 1 / x par le dérivé. Puis d (1 / x) / dx = ─1 / x ^2. Par conséquent dy = ─ Dh / x ^2.

Différentiels fonctions algébriques de base sont donnés ci-dessous.

calculs approximatifs à l'aide de différentiel

Pour évaluer la fonction f (x), et son dérivé f « (x) en x = a est souvent difficile, mais à faire de même dans le voisinage de x = a n'est pas facile. Viennent ensuite à l'aide de l'expression approximative

f (a + AH) ≈ f « (a) Dh + f (a).

Cela donne une valeur approximative de la fonction en petits incréments au travers de son différentiel Ah f « (a) Ah.

Par conséquent, cette formule donne une expression approximative de la fonction au point d'extrémité d'une partie d'une longueur Ah comme une somme de sa valeur au point de départ de la partie (x = a) et l'écart dans le même point de départ. La précision de la méthode de détermination des valeurs de la fonction ci-dessous illustre le dessin.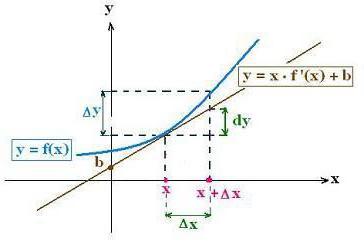

Toutefois connu et l'expression exacte de la valeur de la fonction x = a + Dh donné par la formule incréments finis (ou, en variante, la formule de Lagrange)

f (a + AH) ≈ f « (ξ) Ah + f (a),

où le point x = a + ξ est dans l'intervalle de x = a x = a + Dh, bien que sa position exacte est inconnue. La formule exacte permet d'évaluer l'erreur de la formule approximative. Si l'on met dans la formule Lagrange ξ = Dh / 2, bien qu'il cesse d'être précis, mais donne, en règle générale, une approche beaucoup mieux que l'expression originale en termes de différentiel.

formules d'évaluation d'erreur en appliquant différentiel

Instruments de mesure , en principe, imprécis, et apporter aux données de mesure correspondant à l'erreur. Elles sont caractérisées par la limitation de l'erreur absolue, ou, en bref, l'erreur de fin de course – positif, dépassant clairement l'erreur en valeur absolue (ou au plus égale à elle). Limitation de l'erreur relative est appelé le quotient obtenu en divisant par la valeur absolue de la valeur mesurée.

Soit la fonction exacte formule y = f (x) utilisé pour vychislyaeniya y, mais la valeur de x est le résultat de la mesure, et apporte donc l'erreur de y. Ensuite, pour trouver l'erreur absolue limite │Δu│funktsii y, en utilisant la formule

│Δu│≈│dy│ = │ f « (x) ││Δh│,

où │Δh│yavlyaetsya argument erreur marginal. │Δu│ quantité doit être arrondie vers le haut, comme calcul inexacte lui-même est le remplacement de l'incrément sur le calcul différentiel.